Question

Find the relative rate of change of the function f(t) = 6.5t-10 usingdthe formula In f(t).dtainsdIn f(t)=dt

Answer 1

`f(t)=6.5t^(-10)`

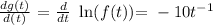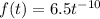
then we have a new function:

`g(t)\text{ = }ln(6.5t^(-10)\text{)}`

its derivative is: the derivative of the outer function (natural logarithm) times the derivative of the inner function 6.5t^-10

that is:

`(dg(t))/(d(t))\text{ = }(1)/(6.5t^(-10))\frac{d}{d\text{ t}}\text{( }6.5t^(-10))^(\square)`

the above because the derivative of the function ln is 1 / x , where in this case x = 6.5t^-10.

The above equation is equivalent to:

`(dg(t))/(d(t))\text{ = }(1)/(6.5t^(-10))\text{( -10 x}6.5t^(-11))^(\square)=\text{ }(1)/(6.5t^(-10))\text{( -}65t^(-11))=-10t^(-1)`

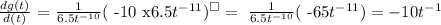
So the correct answer is:

`(dg(t))/(d(t))\text{ = }(d)/(dt)\text{ }\ln (f(t))\text{= }-10t^(-1)`