Question

Use the chinese remainder theorem to solve the systems of congruences:

a. find x mod 77 if x ≡ 2 (mod 7) and x ≡ 4 (mod 11).
b. x ≡ 2 (mod 3), x ≡ 3 (mod 4), x ≡ 1 (mod 5).

Answer 1

(a) Suppose we let


`x=2+4=6`

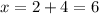
Modulo 7, we're left with
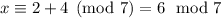
`x\equiv2+4\pmod7=6\mod7`, but we want a remainder of 2, so multiply 4 by 7 to assure that that remainder vanishes. So now


`x=2+4\cdot7=30`

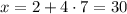
and
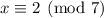
`x\equiv2\pmod7`, but modulo 11, we have
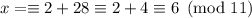
`x=\equiv2+28\equiv2+4\equiv6\pmod{11}`. But we want the remainder to be 4, so multiply the first term by 11 to guarantee this. So we write


`x=2\cdot11+4\cdot7=50`

but now, we get a remainder of 1 modulo 7 and 6 modulo 11. To fix the first case, multiply the first term by 2. For the second case, first find the inverse of 6 modulo 11. We have
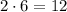
`2\cdot6=12`, and
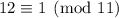
`12\equiv1\pmod{11}`, so the inverse is 2. Multiply the second term by 2, so that the second term's remainder modulo 11 becomes 1. Then multiply by 4, so that now


`x=2\cdot11\cdot2+4\cdot7\cdot2\cdot4=268`

We have


`x=268=3\cdot77+37\implies x\equiv37\pmod{77}`

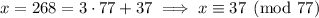
(b) This is done similarly. Modulo 3, we want a remainder of 2, so we can start with


`x=2+3+3=8`

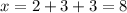
Then taken modulo 4, we need to multiply the first term by 2 and the third term by 4 to ensure the remainder becomes 3. The second term can be left alone.


`x=2\cdot2+3+3\cdot4=19`

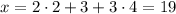
Now taken modulo 5, we can multiply the first two terms by 5 and the third term by the inverse of
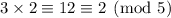
`3*2\equiv12\equiv2\pmod5`. We have
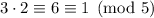
`3\cdot2\equiv6\equiv1\pmod5`, so we multiply by 3.


`x=2\cdot2\cdot5+3\cdot5+3\cdot4\cdot3=71`

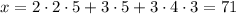
Now


`x=71=1\cdot(3\cdot4\cdot5)+11=1\cdot60+11`

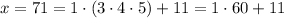
which means the smallest positive solution for the system would be
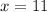
`x=11`.