Question

Write an equation of the line containing the point (3,1) and perpendicular to the line 4x−3y=5.

Answer 1

The given line is 4x - 3y = 5.
Write the equation in standard form.
3y + 5 = 4x
3y = 4x - 5

`y= (4)/(3)x- (5)/(3)`
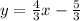
This is a straight line with slope = 4/3, and with y-intercept = - 5/3.

A perpendicular line should have a slope of -3/4, because the product of the slopes of two perpendicular lines is -1.
Let the perpendicular line be

`y=- (3)/(4)x+b`
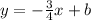
Because the line passes through the point (3,1), therefore

`- (3)/(4)(3)+b=1 \\\\ - (9)/(4)+b=1 \\\\ b=1+ (9)/(4)= (13)/(4)`
The equation of the perpendicular line is

`y=- (3)/(4)x+ (13)/(4)`

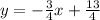
The equation may also be written as
4y + 3x = 13.
A graph of the two lines is shown below.

Answer:

`y=- (3)/(4)x+ (13)/(4) \,\, or \,\, 4y+3x=13`