Question

Opening up the monthly cell phone bill can be alarming due to the uncertainty of the bill. suppose the amount of minutes used per month is distributed normally with a mean of 700 minutes and a standard deviation of 120 minutes. what is the probability that more than 940 minutes were used?

Answer 1

Given the mean of 700 min. and the std. dev. of 120 min., we need to find the z-score for 940 minutes and then the area under the std. normal curve to the right of that z-score.
940 - 700
The applicable z score here is z = ----------------- = 2. What is the area under
120
the curve and to the right of 2 std. deviations from the mean?

You could find the answer from a table of z-scores, or you could take advantage of the empirical rule. The empirical rule states that 95% of the normally distributed data set lies within 2 std. dev. of the mean.

The area to the right of z=2 is 0.5 (half the area under the std. normal curve) less 0.95/2, that is, less 0.475.

Subtracting 0.475 from 0.500 yields 0.025 (answer). 2.5% of the time, the monthly phone bill will exceed 940, or 2 std. dev. above the mean.

Answer 2

the required probability = 0.25

Explanation:

Mean = 700 minutes , Standard Deviation = 120 minutes

To find : the probability that more than 940 minutes were used.

Solution : First find the z-score for 940 minutes and then find the area under the curve to the right of associated standard deviations from the mean.

`z-score=(\mu_2-\mu_1)/(\sigma)\\\\\mu_1=700,\mu_2=940,\sigma=120\\\\\implies z-score=(940-700)/(120)\\\\\implies z-score=2`

Now, calculate the area under the curve to the right of 2 standard deviations from the mean.

Take confidence level to be 95%.

The area to the right of 2 standard deviations is 0.5 that is half the area under the standard normal curve.

`\implies Area < (0.95)/(2)\\\\\implies Area<0.475`

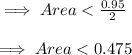
Now, to find the probability that more than 940 minutes were used = 0.5 - 0.475 = 0.25

Hence, the required probability = 0.25