Question

What is the radius of a circle whose equation is x2 + y2 + 8x – 6y + 21 = 0?

Answer 1

radius=2
center(-2,4)

Answer 2

Answer: The required center of the given circle is 2 units.

Step-by-step explanation: We are given to find the radius of a circle with the following equation:

`x^2+y^2+8x-6y+21=0~~~~~~~~~~~~~~~~~~~~~~~(i)`

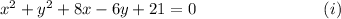
The standard equation of a CIRCLE with radius 'r' units and center at the point (h, k) is given by

`(x-h)^2+(y-k)^2=r^2.`

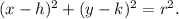
From equation (i), we have

`x^2+y^2+8x-6y+21=0\\\\\Rightarrow (x^2+8x+16)+(y^2-6y+9)-16-9+21=0\\\\\Rightarrow (x^2+2* x* 4+4^2)+(y^2-2* x* 3+3^2)-4=0\\\\\Rightarrow (x+4)^2+(y-3)^2=4\\\\\Rightarrow (x-(-4))^2+(y-3)^2=2^2.`

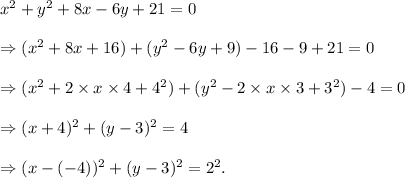
Comparing the above equation with the standard equation (i), we get

radius, r = 2 units and center, (h, k) = (-4, 3).

Thus, the required center of the given circle is 2 units.