Question

Can you please help me solve this problem:Write an equation in slope intercept form, but if it can’t be written in that form write it in standard form.27. Passes through the point (-3,2) and is perpendicular to the line 2x-4y=10

Answer 1

We are given the point (-3,2). We want the equation of the line that passes through this point and that is perpendicular to the line 2x-4y=10.

First, to solve this problem, we will write the given line equation in the slope -intercept form That is:

`2x\text{ -4y=10}`

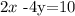
we subtract 10 on both sides to get

`2x\text{ -4y -10=0}`

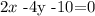
now, we add 4y on both sides to get

`2x\text{ -10=4y}`

Finally we divide both sides by 4, so we get

`y=\frac{2x\text{ -10}}{4}=(x)/(2)\text{ -}(10)/(4)`

from this equation, we can see that the slope of the given line is 1/2.

Now, to calculate the line we will use the following fact. The product of the slopes of two perpendicullar lines is -1.

Let m be the slope of the line we are looking for. Due to this fact we have the equation

`m\cdot(1)/(2)=\text{ -1}`

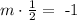
so if we multiply both sides by 2, we get that

`m=\text{ -2}`

so now we know that the slope of the line should be -2.

So we know that the slope is -2 and that is passes through the point (-3,2). Then, we use this formula

`y\text{ - y\_0= m\lparen x -x\_0\rparen}`

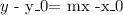
where (x0,y0) is the point through which the liness passes. That is, in our case (-3,2). So we get

`\begin{gathered} y\text{ - 2= -2\lparen x -\lparen-3\rparen\rparen} \\ y\text{ -2= -2\lparen x+3\rparen} \end{gathered}`

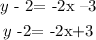
now we add 2 on both sides, so we get

`y=\text{ -2\lparen x+3\rparen+2}`

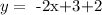
if we distribute the product, we get

`y=\text{ -2x -6 +2= -2x -4}`

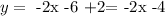
so the equation of the line is y=-2x-4