Question

If a(x) = 3x + 1 and b(x)= √x-4 , what is the domain of (b*a)(x)

Answer 1

a(x) = 3x + 1
b(x) = √(x-4)

Therefore

`(b \circ a) (x) = √(3x+1-4) =√(3x-3)`
This composition of functions is only defined as a real number when x≥0.
Therefore its domain is x = [1,∞]

Answer: [1,∞]

Answer 2

Answer: The correct option is C. The domain of
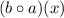`(b\circ a)(x)` is
`[0,\infty)`.

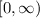Step-by-step explanation:

It is given that,

`a(x)=3x+1`

`b(x)=√(x-4)`

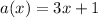
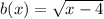
First we have to find the composite function
`(b\circ a)(x)`.

`(b\circ a)(x)=b(a(x))`

`(b\circ a)(x)=b(3x+1)`

`(b\circ a)(x)=√(3x+1-4)`

`(b\circ a)(x)=√(3x-3)`

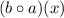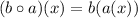
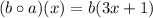
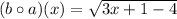
We know that a root function is defined for only positive values therefore the composite function is defined if,

`3x-3\geq 0`

`3x\geq 3`

`x\geq 1`

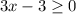
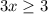
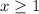
The function is defined for all the values of x which are greater than or equal to 1. Therefore the domain of
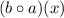`(b\circ a)(x)` is
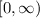`[0,\infty)` and option C is correct.