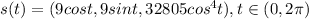Question

Use cos(t) and sin(t), with positive coefficients, to parametrize the intersection of the surfaces x^2+y^2=81 and z=5x^4.

Answer 1

x = 9cos(t)
y = 9sin)t)
z =5[9cos(t)]^4

Answer 2

`s(t)=(9 cost,9 sint , 32805 cos^4 t) , t\in (0,2\pi)`

Explanation:

We are given that two surfaces

`x^2+y^2=81`

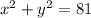
and
`z=5x^4`

We have to find the parametrize the intersection of the given surfaces using cost and sin t with positive coefficient.

We know that intersection curve S(t) is given by

S(t)=(x(t),y(t),z(t)),
`t\in(0,2\pi)`

`x^2+y^2=(9)^2`

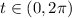
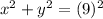
Compare with the equation of circle
`(x-h)^2+(y-k)^2=r^2`

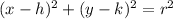
Where (h,k) is center of circle and r is the radius of the circle.

The center and radius of given circle is (0,0) and 9.

`x=9cost,y=9 sint`

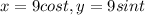
because cost takes along x - axis and sin t takes along y- axis.

When we substitute these values then we get

`81cos^2t+81sin^2t=81(cos^2t+sin^2t)=81` (
`sin^2t+cos^2t)=1`)

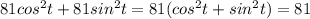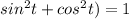Hence,
`x=9 cost, y= 9sint`

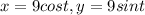
Substitute the value of x in second equation of surface

`z=5(9cost)^4=32805 cos^4t`

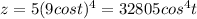
Hence, the intersection curve s(t) is given by

`s(t)=(9 cost,9 sint , 32805 cos^4 t) , t\in (0,2\pi)`