Question

An investment is currently worth 1.035×108 dollars . Thirty years ago, the investment was worth ​ 2.3×105 ​ dollars. How many times greater is the value of the investment today than the value of the investment thirty years ago? A. 0.45 B.450 C.4500 D. 45,000

Answer 1

Answer: B. 450

Explanation:

Given: An investment is currently worth =
`1.035*10^8` dollars .

Thirty years ago, the investment was worth =
`​2.3*10^5` ​dollars.

Now, the number of times the value of the investment today than the value of the investment thirty years ago is given by :-

`n=(1.035*10^8)/(​2.3*10^5)\\\\=0.45*10^(8-5)........\text{Since }a^na^m=a^(m+n)\\\\=0.45*10^3\\\\=0.45*1000=450`

Hence, the value of the investment today is 450 times greater than the value of the investment thirty years ago.

Answer 2

The correct option is: B. 450

Explanation

Current value of the investment is
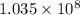`1.035* 10^8` dollars and 30 years ago, the value of the investment was
`2.3* 10^5` dollars.

Suppose, the value of investment today is
`n` times greater than the value of the investment thirty years ago.

So, the equation will be........

`n(2.3* 10^5)=1.035* 10^8\\ \\ n= (1.035* 10^8)/(2.3* 10^5)=0.45* 10^3 = 450`

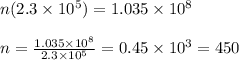
Thus, the value of the investment today is 450 times greater than the value of the investment thirty years ago.