Question

Use the remainder theorem to find P(-3) for P(x) = x* + 2x - 4x +4.Specifically, give the quotient and the remainder for the associated division and the value of P(-3).Quotient =0X 5 ?RemainderP(-3) = 0

Answer 1

Ok, so

We got the polynomial:

`P(x)=x^4+2x^3-4x^2+4`

We are going to find P(-3) using the remainder theorem.

For this, we got that if P(-3), then we can write x+3 as a probable root of the polynomial.

We are going to write the coefficients of each term below, and use the theorem for x=-3.

As the remainder is -5, the value of P(-3) is -5.

The quotient will be:

The quotient is equal to the following function:

`f(x)=x^3-x^2-x+3`

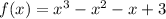
quotient: x^3-x^2-x+3