Question

A line contains the points (−26, −37) and (−32, −61) .

What is the slope of the line in simplified form?



Enter your answer in the box.

Answer 1

The slope is 4
To find the slope formula is y2-y1/x2-y1 so you will have -61- -37 / -32- -26 which will give you 24/ 6 and when you simplify is 4

Answer 2

The slope of the line containing the points (-26,-37) and (-32,-61) is 4

Explanation:

Given:

Two points of the line (-26,-37) and (-32,-61)

To find:

Slope(m) of the line =?

Solution:

The Equation of slope of two points is

`Slope m=((y_2-y_1))/((x_2-x_1))`

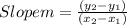
Let (-26,-37) be
`(x_1,y_1)`

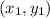
and (-32,-61) be
`(x_2,y_2)`

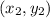
Now substituting the values ,

`m=((-61+37))/((-32+26))`

`m=(-24)/(-6)`

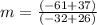
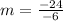
m=4

Thus the slope of the line is 4