If you have a TI-83 plus or higher, you could create a matrix and use rref to get the solution.
Let's begin with eliminating the y's in equations 1 and 3, then in equations 2 and 3:
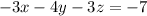
times -1⇒
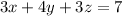

times 2⇒

ADD the two equations: 13x + 13z = 25
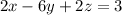
times -1⇒
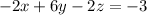

times 3⇒

ADD the two equations: 13x+13z=24
Subtract the two resulting equations and you get 0 = 1 which is false so there is no solution for the system.