Given,
The mass of the block, m=51.0 kg
The angle, θ=-25°
The coefficient of static friction, μ_s=0.1
The coefficient of kinetic friction, μ_k=0.03
(a)
The minimum force that is needed to get the block moving is equal to the static frictional force that acts on the block.
Thus, the minimum force required is,
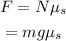
Where N is the normal force acting on the block and g is the acceleration due to gravity.
On substituting the known values,
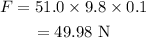
Thus the minimum force needed to get the block moving is 49.98 N
(b)
When the block starts to move, the static friction will no longer act on the block. When the block is moving, the kinetic friction starts to act on the block.
Thus the net force on the block when it starts to move is given by,
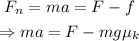
Where f is the kinetic friction acting on the block and a is the acceleration of the block.
On substituting the known values,
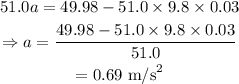
Thus, the acceleration of the block once it starts to move is 0.69 m/s²