Question

What are the amplitude, period, and midline of f(x) = −4 cos(2x − π) + 3?

Answer 1

`\bf \qquad \qquad \qquad \qquad \textit{function transformations} \\ \quad \\ % function transformations for trigonometric functions \begin{array}{rllll} % left side templates f(x)=&{{ A}}sin({{ B}}x+{{ C}})+{{ D}} \\\\ f(x)=&{{ A}}cos({{ B}}x+{{ C}})+{{ D}}\\\\ f(x)=&{{ A}}tan({{ B}}x+{{ C}})+{{ D}} \end{array} \\\\ -------------------\\\\`


`\bf \bullet \textit{ stretches or shrinks}\\ \left. \qquad \right. \textit{horizontally by amplitude } |{{ A}}|\\\\ \bullet \textit{ flips it upside-down if }{{ A}}\textit{ is negative}\\ \left. \qquad \right. \textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if }{{ B}}\textit{ is negative}\\ \left. \qquad \right. \textit{reflection over the y-axis}`


`\bf \bullet \textit{ horizontal shift by }\frac{{{ C}}}{{{ B}}}\\ \left. \qquad \right. if\ \frac{{{ C}}}{{{ B}}}\textit{ is negative, to the right}\\\\ \left. \qquad \right. if\ \frac{{{ C}}}{{{ B}}}\textit{ is positive, to the left}\\\\ \bullet \textit{vertical shift by }{{ D}}\\ \left. \qquad \right. if\ {{ D}}\textit{ is negative, downwards}\\\\ \left. \qquad \right. if\ {{ D}}\textit{ is positive, upwards}`


`\bf \bullet \textit{function period or frequency}\\ \left. \qquad \right. \frac{2\pi }{{{ B}}}\ for\ cos(\theta),\ sin(\theta),\ sec(\theta),\ csc(\theta)\\\\ \left. \qquad \right. \frac{\pi }{{{ B}}}\ for\ tan(\theta),\ cot(\theta)`

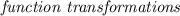
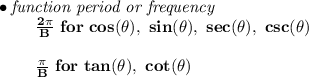
with that template in mind, let's check


`\bf f(x)=-\stackrel{A}{4}(\stackrel{B}{2}x\stackrel{C}{-\pi } )\stackrel{D}{+3}\\\\ -------------------------------\\\\ Amplitude\implies 4\\\\ Period\implies \cfrac{2\pi }{B}\implies \cfrac{2\pi }{2}\implies \pi`

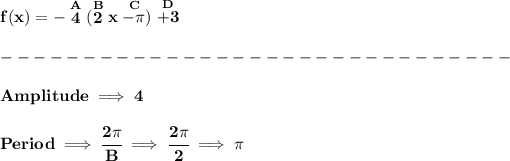
now, the function is just the parent cos(x), shrunk some, -4, and shifted about, now D = +3, that means it has a vertical shift of 3 units up.

the parent function cos(x), has a midline of y = 0, now, if we shift it upwards by 3 units, the new midline will then be y = 3.