Question

Select the correct point (x,y) on the unit circle that corresponds to tan (7π/3)

Answer 1

On a unit circle, the coordinates of a point (x, y) are given to be:

`(x,y)=(\cos \theta,\sin \theta)`

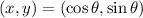
The sign of the coordinates is dependent on the location of the point, that is the quadrant in which the reference angle is located.

The question gives that the point corresponds to:

`\tan ((7\pi)/(3))`

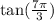
Therefore, this means that the angle will be:

`\theta=(7\pi)/(3)`

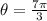
The angle is greater than a complete revolution, 2π. Therefore, we have to find the measure of the angle in the first revolution. we will subtract 2π from the angle. Therefore:

`\theta=(7\pi)/(3)-2\pi=(7\pi-6\pi)/(3)=(\pi)/(3)`

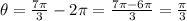
Therefore, the angle is π/3. This is a special angle and is located in the first quadrant. This means that the coordinates are both positive.

Using the special identity of π/3, we have that:

`\begin{gathered} \sin ((\pi)/(3))=\frac{\sqrt[]{3}}{2} \\ \cos ((\pi)/(3))=(1)/(2) \end{gathered}`

Therefore, the point on the unit circle will be given to be:

`\begin{gathered} \text{Since} \\ (x,y)=(\cos \theta,\sin \theta) \\ \text{then} \\ (x,y)=((1)/(2),\frac{\sqrt[]{3}}{2}) \end{gathered}`

The correct option is OPTION A.