Question

A general contractor is constructing a building that requires a concrete foundation that is to be 20 feet by 12 feet and 4 inches thick. if the local home supply store sells concrete for $125 per cubic yard, what will be the cost of the concrete for the foundation?

Answer 1

$370.37.

Explanation:

We have been given that a general contractor is constructing a building that requires a concrete foundation that is to be 20 feet by 12 feet and 4 inches thick.

First of all, we will convert the given dimensions of foundation in yards.

`\text{3 feet}=\text{1 yard}`

`20\text{ feet}=(20)/(3)\text{ yards}`

`12\text{ feet}=(12)/(3)\text{ yards}`

`\text{36 inches}=\text{1 yard}`

`\text{4 inches}=(4)/(36)\text{ yards}=(1)/(9)\text{ yards}`

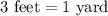
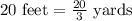
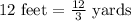
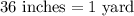
Since the foundation of building is in form of cuboid, so volume of foundation will be the product of 3 sides.

`\text{Volume of foundation}=(20)/(3)\text{ yards}* (12)/(3)\text{ yards}* (1)/(9)\text{ yards}`

`\text{Volume of foundation}=(20* 12* 1)/(3* 3 * 9)\text{ yards}^3`

`\text{Volume of foundation}=(240)/(81)\text{ yards}^3`

`\text{Volume of foundation}=2.962962962962963\text{ yards}^3`

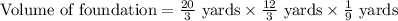
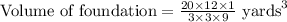
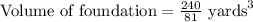
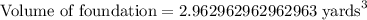
Since the local home supply store sells concrete for $125 per cubic yard, so the cost of the concrete for the foundation will be the volume of foundation times $125.

`\text{The cost of the concrete for the foundation}=2.962962962962963\text{ yards}^3* \frac{\$125}{\text{ yards}^3}`

`\text{The cost of the concrete for the foundation}=\$370.37037\approx \$370.37`

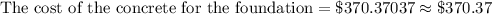
Therefore, the cost of the concrete for the foundation is $370.37.

Answer 2

First we calculate the volume of the foundation:

Volume (V) = 20 ft * 12 ft * 4 in (1 ft / 12 in)

V = 80 ft^3

Since the cost is in cubic yard (yard^3) so convert:

V = 80 ft^3 * (1 yard^3 / 27 ft^3) = 2.963 yard^3

So the total cost is:

cost = ($125 / yard^3) * 2.963 yard^3

cost = $370.37