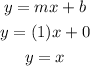Question

In the xy-plane, points A and B have coordinates (-2,0) and (0,2), respectively. What is an equation ofthe line that passes through the origin and is parallel to line segment AB ?O y = xOy= -xO y = 2xOy=2x-2

Answer 1

On the coordinate grid, the points A and B have the following coordinates;

`\begin{gathered} A=(-2,0) \\ B=(0,2) \end{gathered}`

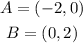
We would begin by calculating the slope of thi line as shown below;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \text{Where;} \\ (x_1,y_1)=(-2,0) \\ (x_2,y_2)=(0,2) \\ m=(2-0)/(0-\lbrack-2\rbrack) \\ m=(2)/(0+2) \\ m=(2)/(2) \\ m=1 \end{gathered}`

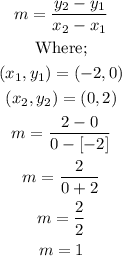
The slope of the line AB equals 1.

For two lines to be parallel on the coordinate grid, then they both must have the same slope. Thi means, the line that passes through the origin also has a slope of 1.

Also, for the line to pass through the origin, that means one of its points has the coordinates (0, 0).

Therefore, for a line with one of its points given as (0, 0) and its slope is 1, the equation would be;

`\begin{gathered} \text{The equation of the line in slope-intercept form would be;} \\ y=mx+b \\ \text{Substitute for the values of }x,y\text{ and m} \\ 0=1(0)+b \\ 0=0+b \\ b=0 \end{gathered}`

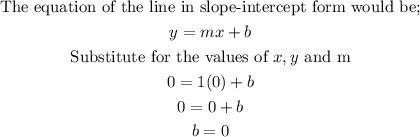
With the slope determined as 1, and the y-intercept determined as 0, the equation therefore would be;

`\begin{gathered} y=mx+b \\ y=(1)x+0 \\ y=x \end{gathered}`