Question

Find the asymptotes and intercepts of the function. g(x) = (x-2) / x^2 - 2x - 3

Answer 1

`\bf g(x)=\cfrac{x^2}{x^2-2x-3}`

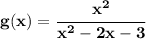
so, notice, the degree of the numerator is the same degree as the denominator's, therefore the horizontal asymptote is at


`\bf g(x)=\cfrac{1x^2}{1x^2-2x-3}\implies \cfrac{1}{1}\implies \stackrel{\textit{horizontal asymptote }y=1}{1}`

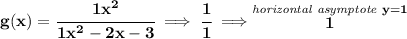
the vertical asymptotes are at the zeros of the denominator, let's check.


`\bf x^2-2x-3=0\implies (x-3)(x+1)=0\implies x= \begin{cases} 3\\ -1 \end{cases}`

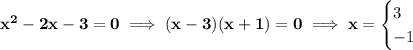
there are no oblique or slanted asymptotes, that only occurs when the numerator's degree is higher by 1.

to get the x-intercept, simple enough, just set y = 0 and solve for "x" as usual.


`\bf \stackrel{0}{g(x)}=\cfrac{x^2}{x^2-2x-3}\implies 0=\cfrac{x^2}{x^2-2x-3}\implies \boxed{0=x}`

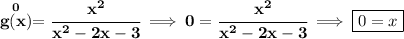
and to get the y-intercept, set x = 0, and solve for "y".


`\bf g(x)=\cfrac{0^2}{0^2-2(0)-3}\implies g(x)=\cfrac{0}{-3}\implies \boxed{g(x)=0}`