so, after 15 minutes A has leaked 2/3 of a gallon, how much will it be for 20 minutes? let's see.
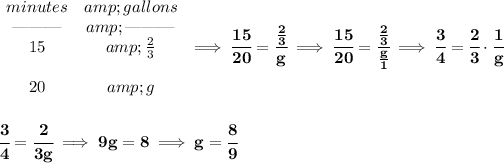
so in 20 minutes A has leaked that much, which is larger, 8/9 or 3/4?
let's multiply each fraction by "the other's denominator", to make them the same denominator.

so, which one do you think is larger? well, that is the one that's leaking faster, because is leaking more gallons per minute.