Question

Estimate the area under the curve f(x) = x^2 from x = 1 to x = 5 by using four inscribed (under the curve) rectangles. Answer to the nearest integer.

Answer 1

30 square units

Explanation:

For a rectangle to be described as "inscribed" in the context of estimating the area under a curve, the entire rectangle should be positioned underneath the curve.

Therefore, as the curve of f(x) = x² is convex (concave up) in the interval [1, 5], to estimate the area under the curve by using inscribed rectangles, we can use the Left Riemann Sum.

The Left Riemann Sum is a numerical approximation method used to estimate the definite integral of a function over a given interval by dividing the interval into subintervals. It approximates the area under the curve of a function by using rectangles, where the left side of each rectangle touches the curve at the left endpoint of each subinterval.

`\boxed{\begin{minipage}{11cm}\underline{Left Riemann Sum}\\\\$\displaystyle \int^b_a f(x)\; \text{d}x \approx \Delta x \left(f(x_0)+f(x_1)+f(x_2)+...+f(x_(n-2))+f(x_(n-1))\right)$\\\\$\text{where}\; \Delta x=(b-a)/(n)$\\\end{minipage}}`

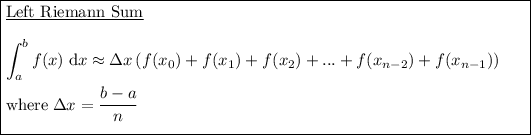
The number of subintervals, n, is the number of rectangles used, and the interval is [a, b].

As the interval is [1, 5], this means that a = 1 and b = 5.

As the number of rectangles to use is 4, then n = 4.

Calculate the value of Δx:

`\Delta x=(b-a)/(n)=(5-1)/(4)=(4)/(4)=1`

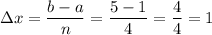
The given partition divides the interval [1, 5] into 4 subintervals where the width of each subinterval is one. Therefore, the left endpoints are:

• 
  `x_0=1`
• 
  `x_1=2`
• 
  `x_2=3`
• 
  `x_3=4`

Substitute everything into the formula and solve:

`\begin{aligned}\displaystyle \int^5_1 x^2\; \text{d}x &\approx 1\cdot \left(f(1)+f(2)+f(3)+f(4))\right)\\\\&=(1)^2+(2)^2+(3)^2+(4)^2\\\\&=1+4+9+16\\\\&=30\end{aligned}`

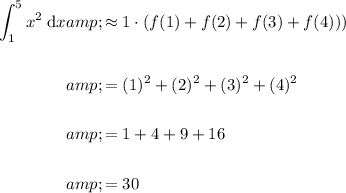
Therefore, the estimation of the area under the curve f(x) = x² from x = 1 to x = 5 using four inscribed rectangles is 30 square units.