Answer:
The correct option is C.
Explanation:
The given equation of curve is

We need to find the area under the given curve from x = 0 to x = 4 using 4 rectangles and left endpoints.
We have 4 rectangles in x = 0 to x = 4. So,
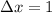
Left Riemann sum:
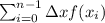
Using Left Riemann sum, we get
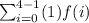
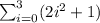
![[\because y=2x^2+1]](https://img.qammunity.org/2018/formulas/mathematics/high-school/iqd9gzp41g2v3fknuish7eoxctr4jrs69l.png)
The area under the given curve from x = 0 to x = 4 using 4 rectangles and left endpoints is
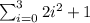
Therefore the correct option is C.