Question

Write an equation for the linear function satisfying the given conditions f(-3)=5 and f(6)=-2

Answer 1

The two points (-3,5) and (6,-2) are on this line. Using the slope formula, we get
m = (y2-y1)/(x2-x1)
m = (-2-5)/(6-(-3))
m = (-2-5)/(6+3)
m = -7/9
-------------------------------
Now use this slope value, and the point (x,y) = (-3,5), to find the y intercept b

y = mx+b
5 = (-7/9)(-3)+b
5 = 7/3+b
5-7/3 = 7/3+b-7/3
8/3 = b
b = 8/3
-------------------------------

We go from y = mx+b to y = (-7/9)x + 8/3

So the linear function is
`f(x) = -(7)/(9)x+(8)/(3)` which is the final answer

-------------------------------

Check:
Plug in x = -3

`f(x) = -(7)/(9)x+(8)/(3)`


`f(-3) = -(7)/(9)(-3)+(8)/(3)`


`f(-3) = (7)/(3)+(8)/(3)`


`f(-3) = (7+8)/(3)`


`f(-3) = (15)/(3)`


`f(-3) = 5`

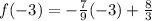
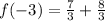
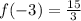
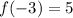
So that checks out.

----------

Plug in x = 6


`f(x) = -(7)/(9)x+(8)/(3)`


`f(6) = -(7)/(9)(6)+(8)/(3)`


`f(6) = -(14)/(3)+(8)/(3)`


`f(6) = (-14+8)/(3)`


`f(6) = (-6)/(3)`


`f(6) = -2`

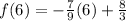
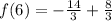
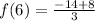
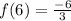
and that checks out at as well. The answer has been fully confirmed.