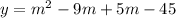Question

An equation has solutions of m = –5 and m = 9. Which could be the equation?

Answer 1

`\bf \begin{cases} m=-5\implies &m+5=0\\ m=9\implies &m-9=0 \end{cases}\implies (m+5)(m-9)=\stackrel{original}{polynomial} \\\\\\ m^2-9m+5m-45=y\implies m^2-4m-45=y`

Answer 2

`y=m^2-4m-45`

Explanation:

An equation has solutions of m = –5 and m = 9

WE are given with the solution. Lets write the solution as factors

When x=a is a solution then factor is (x-a)

`m=-5` is a solution. change the sign of the solution while writing factor. factor is (m+5)

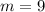`m=9` is a solution, factor is (m-9)

we use the factors to find the equation

`y=(m+5)(m-9)`

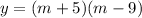
Multiply the factors using FOIL method

`y=m^2-9m+5m-45`

`y=m^2-4m-45`