Question

what value in place of the question mark makes the polynomial below a perfect square trinomial 9x^2+?x+49

Answer 1

hello :
9x²+ bx +49 = (3x)² +2(3x)(7) +7²
so : b = 42
9x²+42x+49 = ( 3x+7)²....( perfect square trinomial)

Answer 2

The required value is 42 which makes the polynomial a perfect square trinomial.

Explanation:

Given the trinomial

`9x^2+?x+49`

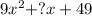
we have to find the value in the place of question mark which makes the polynomial above a perfect square trinomial.

By the identity of perfect square

`a^2+2ab+b^2=(a+b)^2`

`\text{Here given the polynomial with above identity }9x^2+?x+49`

`(3x)^2+?x+7^2`

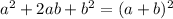
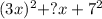
which given a=3x, b=7

Hence, put these values in identity we get

`(3x)^2+2(3x)7+7^2=(3x+7)^2`

`9x^2+42x+49=(3x+7)^2`

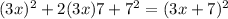
Hence, the required value is 42 which makes the polynomial a perfect square trinomial.