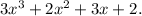Question

If f(x) = 3x + 2 and g(x) = x2 + 1, which expression is equivalent to (f*g) (x)?

Answer 1

Answer: The required expression is
`3x^3+2x^2+3x+2.`

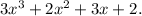
Step-by-step explanation: We are given the following two functions :

`f(x)=3x+2\\\\g(x)=x^2+1.`

We are to find the expression equivalent to
`(f*g)(x).`

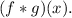
We know that

for any two functions p(x) and q(x), we have

`(p*q)(x)=p(x)* q(x).`

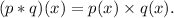
Therefore, we get

`(f*g)(x)\\\\=f(x)* g(x)\\\\=(3x+2)(x^2+1)\\\\=x^2(3x+2)+1(3x+2)\\\\=3x^3+2x^2+3x+2.`

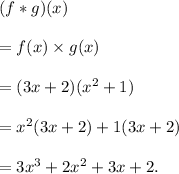
Thus, the required expression is
`3x^3+2x^2+3x+2.`

Answer 2

(f*g) (x) = (3x + 2) (x^2 + 1)
(f*g) (x) = 3x^3 + 3x + 2x^2 + 2
(f*g) (x) = 3x^3 + 2x^2 + 3x + 2