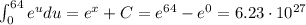Question

Evaluate ſ3x? exi dx 0 4 ( 3x² ex dx = 0 (Type an exact answer.)

Answer 1

We have to solve the integral:

`\int ^4_03x^2e^(x3)dx`

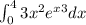
(Note: the editor does not let write x^3 as the exponent of e)

We will have to do a substitution of variables in order to simplify the solution.

For example, we can see that the derivative of x^3 is 3x^2, that is the factor that multiplies the exponential function. This tells us a clue about a possible substitution.

So we will try the following substitution:

`\begin{gathered} u=x^3\Rightarrow du=3x^2\cdot dx \\ x=0\Rightarrow u=0^3=0 \\ x=4\Rightarrow u=4^3=64 \end{gathered}`

Then:

`\int ^4_03x^2e^(x3)dx=\int ^4_0e^(x3)(3x^2dx)=\int ^(64)_0e^udu`

We can solve this integral as:

`\int ^(64)_0e^udu=e^x+C=e^(64)-e^0=6.23\cdot10^(27)`