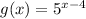Question

Which function represents a horizontal shift of f(x)=5^x by 4 units to the right?

Answer 1

Answer:
`g(x)=5^(x-4)`

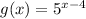
Explanation:

When a function f(x) is shifted horizontally by n units to the right , the new function will become :-

`g(x)=f(x-n)`

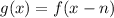
The given function :
`f(x)=5^x`

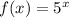
Now, if the given function shifted 4 units to the right , then the new function will become :

`g(x)=f(x-4)`

`g(x)=5^(x-4)`

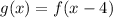
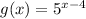
Hence, the function represents a horizontal shift of
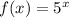`f(x)=5^x` by 4 units to the right will be :-

`g(x)=5^(x-4)`

Answer 2

If you have a function y = f(x), the transformation along the x-axis is given by:

y = f(x+a) ⇒ This is the translation to the LEFT by 'a' units
y = f(x-a) ⇒ This is the translation to the RIGHT by 'a' units

So you have, f(x) = 5ˣ, translated 4 unit right will give g(x) = 5⁽ˣ⁻⁴⁾