Quadrilateral ABCD is inscribed in a circle. Let the measure of arc BAD be a°. Arcs BCD and BAD form a circle and a circle measures 360°, then measure of arc BCD is 360°-a°.
The inscribed angle theorem states that an angle inscribed in a circle is half of the central angle that subtends the same arc on the circle.
Because of the Inscribed angle theorem,
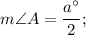

The sum of the measures of angles A and C is
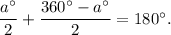
Therefore, angles A and C are supplementary, because their measures add up to 180°.
Angles B and D are supplementary, because the sum of the measures of the angles in a quadrilateral is 360°.
m∠A + m∠C + m∠B + m∠D = 360°,
and using substitution,
180° + m∠B + m∠D = 360°, so m∠B + m∠D = 180°.
Answer: inscribed angle theorem