Question

A charge of 40 µC is pushed by a force of 15 µN a distance of 1.3 mm in an electric field. What is the electric potential difference?

Answer 1

C. 4.9 × 10-4 V

Step-by-step explanation:

ΔV = E d

E = force/charge = 15 µN / 40 µC = 0.375 N/C

ΔV = 0.375 N/C * 0.0013 m = C. 4.9 × 10-4 V

Answer 2

ΔV=V1-V2 = 27692307.69volts

Step-by-step explanation:

Hello! Let's solve this!

The formula to calculate the power difference is

ΔV=V1-V2

V = k * (q / r)

k is a constant that equals
`k=9*10^(9)N*m^(2)/C^(2)`

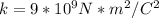
The data we have are:

`k=9*10^(9)N*m^(2)/C^(2)`

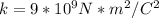
r = 0.0013m

`q1=40*10^(-6)C\</p><p>F=15*10^(-6)  N`

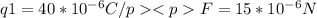
From the following formula we can calculate how much q2 is

F = k * (q1 * q2 / r2)

q2 = (F * r2) / (k * q1)

q2 = (15*10^{-6} N[/tex] * 0.00132) / (9*10^{9}N*m^{2}/C^{2}[/tex] *40*10^{-6}C\)

`q2=7.0417x^(-17)C`

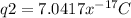
Now we calculate with q1 and q2, V1 and V2 respectively.

V1 = (9*10^{9}N*m^{2}/C^{2}[/tex] * 40*10^{-6}C\) /0.0013m

V1 = 27692307.69 volts

V2 = (9*10^{9}N*m^{2}/C^{2}[/tex] * 7.0417x^{-17}C[/tex]) /0.0013m

`V2=4.875*10^(-4)volts`

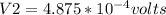
Then we solve the potential difference:

V1-V2 = 27692307.69 volts-4.875*10^{-4}volts[/tex]

ΔV=V1-V2 = 27692307.69volts