Question

Determine the intervals on which the polynomial is entirely negative and those on which it is entirely positive. (Enter your answers using interval notation. Enter EMPTY or ∅ for the empty set.)

−x^2 + 6x − 10
I don't understand how to factor this, as as such, I can't figure out how to answer the question. Please help!

Answer 1

This is a parabola that opens downward.
Remember that the axis of symmetry is located at x=-b/(2a).
So the vertex is at (3,-1)
So functions slope is positive or increasing on (-co, 3] and decreasing on [3,co).

Answer 2

Answer with explanation:

The function for which we have to find , the intervals on which the polynomial is entirely negative and those on which it is entirely positive.

f(x)= -x²+6 x -10

If you will find the root of the function, there is no real root.

To find the root we will use Discriminant formula

For a Quadratic function, ax²+b x+c=0,

`x=(-b+√(D))/(2a)\\\\D=b^2-4ac\\\\x=(-6\pm √(6^2-4 *(-1)*(-10)))/(2*(-1))\\\\x=(-6\pm√(-4))/(-2)`

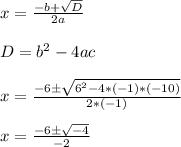
→So,there is no interval in which the polynomial is entirely negative and those on which it is entirely positive, which can be represented in interval notation using Ф.

`f(x)= -(x^2-6x+10)\\\\= - [(x-3)^2-9+10]\\\\=-(x-3)^2-1`

For, any value of x,the value of f(x) will be always Negative.

To find the vertex, put ,x-3=0

x=3

And, by putting , x= 3 ,in the equation we get

y = -1

So,Vertex = (3, -1)

⇒If you will try to find the intervals in which the function is increasing , means the curve is moving up is from (-∞, 3) and the intervals in which the function is decreasing , means the curve is moving downward is from , (3, ∞).