Given:
m∠ADC = 56°
m∠ADB = (x + 7)°
m∠BDC = (2x + 19)°
Let's write and solve an equation to find x.
Since measure of angle ADC is 56 degrees, it means the sum of measures of angle ADB and BDC will be 56 degrees.
To write the equation to solbe for x, we have:
m∠ADB + m∠BDC = m∠ADC
Hence, the equation is:
(x + 7) + (2x + 19) = 56
From the equation above, let's solve for x.
• Remove the parentheses:
x + 7 + 2x + 19 = 56
• Combine like terms:
x + 2x + 7 + 19 = 56
3x + 26 = 56
• Subtract 26 from both sides of the equation:
3x + 26 - 26 = 56 - 26
3x = 30
• Divide both sides by 3:
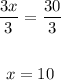
Therefore, the value of x = 10.
To find the measures of angle ADB and BDC, substitute 10 for x in each measure amd evaluate.
• m∠ADB = (x + 7) ==> (10 + 7) = 17,°
• m∠BDC = (2x + 19) ==> (2(10) + 19) = 20 + 19 = 39,°
Therefore, the measure of angle ADB is 17 degrees, while the measure of angle BDC is 39 degrees.
ANSWER:
• x = 10
,
• m∠ADB = 17,°
,
• m∠BDC = 39,°