Question

1. If x-1 is a factor of p(x)=x^3-7x^2+15x-9, which of the following represents the complete factorization for p(x)?

A. (x-3)(x+4)(x+1)
B. (x-3)(x-3)(x-1)
C. (x-3)(x+3)(x-1)
D. (x-3)(x+3)(x+1)

2. The point (1,0) lies on the graph of p(x)=x^4-2x^3-x+2
True or false

Answer 1

1. Option B is the correct answer.

2. The point (1,0) lies on the graph of p(x)=x⁴-2x³-x+2.

Explanation:

1. Dividing x³-7x²+15x-9 with (x-1).

`(x^3-7x^2+15x-9)/(x-1)=x^2-6x+9`

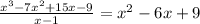
Factorizing x²-6x+9 we will get

x²-6x+9 = (x - 3)(x-3)

x³-7x²+15x-9 = (x-1)(x - 3)(x-3)

Option B is the correct answer.

2. We have p(x)=x⁴-2x³-x+2

That is y = x⁴-2x³-x+2

We have coordinates (1,0), substituting

y = 1⁴-2 x 1³-1+2 = 0

So when we are substituting x value as 1 we are getting y as zero, so the point lies in curve.