Question

Plane A leaves Tulsa at 2:00 p.m., averaging 300 mph and flying in a northerly direction. Plane B leaves Tulsa at 2:30 p.m., averaging 225 mph and flying due east. At 5:00 p.m., how far apart will the planes be?

Answer 1

Answer 1061

Explanation:

Answer 2

At 5:00 p.m. the planes will be
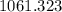`1061.323` miles apart.

Explanation:

To solve this problem, I add a picture of the situation.

We know that speed is distance over time ⇒

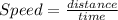`Speed=(distance)/(time)` (I)

The first step to solve this exercise is to graph the situation. We can draw a right triangle which vertices will be ''Tulsa'', and the planes ''A'' and ''B'' at 5:00 p.m.

In order to know the measures of the sides, we are going to calculate them using the equation (I)

Plane A leaves Tulsa at 2:00 p.m.

Therefore, at 5:00 p.m. it will have flown 3 hours ⇒

`300(mi)/(h)=(distance)/(3h)` ⇒

`distance=(300(mi)/(h)).(3h)`

`distance=900mi`

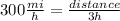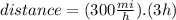
At 5:00 p.m. the distance from the plane A to Tulsa is 900 mi

Plane B leaves Tulsa at 2:30 p.m.

Therefore, at 5:00 p.m. it will have flown 2.5 hours ⇒

`225(mi)/(h)=(distance)/(2.5h)`

`distance=(225(mi)/(h)).(2.5h)`

`distance=562.5mi`

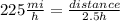
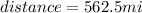
At 5:00 p.m. the distance from the plane B to Tulsa is 562.5 mi

Finally, we can find the distance between the plane A and the plane B using the Pythagorean theorem :

`(900mi)^(2)+(562.5mi)^(2)=(Distance_(A-B))^(2)`

`810000mi^(2)+316406.25mi^(2)=(Distance_(A-B))^(2)`

`(Distance_(A-B))^(2)=1126406.25mi^(2)`

`Distance_(A-B)=\sqrt{1126406.25mi^(2)}`

`Distance_(A-B)=1061.322877mi` ≅
`1061.323mi`

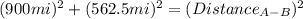
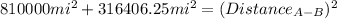
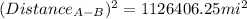
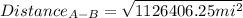
At 5:00 p.m. the planes will be 1061.323 miles apart.