Answer: Second option
 is the correct option.
is the correct option.
Step-by-step explanation:
If two triangles are congruent then their corresponding sides are congruent.
In
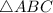 and
and
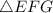 , AB, BC, and CA are corresponding to EF, FG and GE respectively.
, AB, BC, and CA are corresponding to EF, FG and GE respectively.
Therefore, if
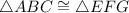 then,
then,
 ,
,
 ,
,
And,

Therefore, only second option is correct.