Question

You are given two vectors to add. Draw the resultant then calculate its magnitude and direction. A small plane is seen moving at 90m/s east while drifting north at a speed of 30m/s due to high winds. What is its overall velocity

Answer 1

Let two vectors A and B makes an angle θ between them. The sum of the vectors or the magnitude of the resultant vector is given as,

`R=\sqrt[]{A^2+B^2+2AB\cos \theta}`

And the direction is given as,

`\alpha=\tan ^(-1)((\lvert B\rvert\sin \theta)/(\lvert A\rvert+\lvert B\rvert\cos \theta))`

Assuming east as positive x direction and north as positive y direction:

Given that,

Velocity of the plane;

`v_p=(90\hat{i})\text{ m/s}`

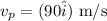
Velocity of the wind;

`v_w=(30\hat{j})\text{ m/s}`

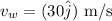
The angle between North and East direction is,

`\theta=90\degree`

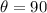
The resultant velocity is given as,

`\begin{gathered} v_r=\sqrt[]{v^2_p+v^2_w+2v_pv_w\cos\theta} \\ =\sqrt[]{\lbrack(90)\rbrack^2+\lbrack(30)\rbrack^2+2\lbrack(90)\rbrack\lbrack(30)\rbrack^{}\cos (90\degree)}\text{ m/s} \\ \approx94.87\text{ m/s} \end{gathered}`

The direction is given as,

`\begin{gathered} \alpha=\tan ^(-1)((\lvert v_w\rvert\sin \theta)/(\lvert v_p\rvert+\lvert v_w\rvert\cos \theta)) \\ =\tan ^(-1)(\frac{\lvert30\hat{j}\rvert\sin (90\degree)}{\lvert90\hat{i}\rvert+\lvert30\hat{j}\rvert\cos (90\degree)}) \\ =\tan ^(-1)((30)/(90)) \\ \approx18.43\degree \end{gathered}`

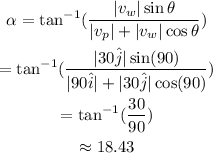
Therefore, the resultant velocity of the plane is 94.87 m/s and is directed 18.43° towards North-East.