The line tangent to (the graph of) a function is horizontal, when it's slope is equal to 0.
The slope of the tangent line at a point, is determined by the derivative of the function, at that point.
So, we find the derivative of f, and find when it is equal to 0:
f'=2cos(x)-2sin(x)
2cos(x)-2sin(x)=0
cos(x)=sin(x),
then x is 45 degrees or 45+180=225 degrees, which are
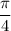
radians, and [tex] \displaystyle{\frac{ 5\pi }{4}
Answer: π/4, 5π/4