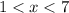Answer:
The solution of the given inequality
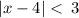 is
is
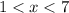
Explanation:
Given inequality
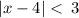
We have to find the solution of the given inequality
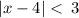
Using absolute rule,
 , we have,
, we have,
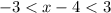
Rewrite as
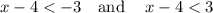
Consider ,
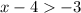
Adding 4 both side, we have,
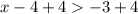
Simplify, we have,
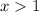
Consider ,
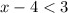
Adding 4 both side, we have,

Simplify, we have,
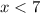
Combining, we have,
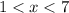
Thus, The solution of the given inequality
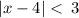 is
is