Answer: The magnitude of the earthquake that is 35 times more intense than a standard earthquake=1.5
Explanation:
Given : The magnitude M of an earthquake is defined to be
 ---(1)
---(1)
, where I is the intensity of the earthquake (measured by the amplitude of the seismograph wave) and
S is the intensity of a “standard” earthquake, which is barely detectable.
If the magnitude of an earthquake that is 35 times more intense than a standard earthquake
⇒Intensity of earthquake I=35 S
Substitute the value of I in (1), we get
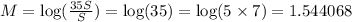

∴ The magnitude of the earthquake that is 35 times more intense than a standard earthquake=1.5