Answer:
For all
 , the graph of given equation have two x-intercepts if the discriminant is positive.
, the graph of given equation have two x-intercepts if the discriminant is positive.
Explanation:
A quadratic equation
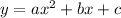 has
has
1. No x-intercept if
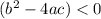 .
.
2.One x-intercept if
 .
.
3. Two x-intercept if
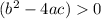 .
.
The given equation is
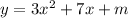
It is a quadratic equation. Here, a=3, b=7 and x=m. The graph of given equation have two x-intercepts if the discriminant is positive.
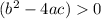
Put a=3, b=7 and x=m in the above inequality.


Add 12m on both the sides.
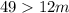
Divide both sides by 12.

For all
 , the graph of given equation have two x-intercepts if the discriminant is positive.
, the graph of given equation have two x-intercepts if the discriminant is positive.