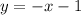Question

Write an equation for the graph below in terms of X 5+ 4 3 2 1 -3 -2 - 7 2 3 -2 -3 -4 -5+ q y =

Answer 1

In order to find the equation of the graph here are some steps that we can follow in order to simplify the work of finding the graph.

1. Appoint 2 points lying in the line to be used as our reference.

2. Find the slope "m" of the line.

3. Using the Slope-Intercept Form find the equation of the line.

So let us begin.

STEP 1. Appoint 2 points.

In our Graph we can see that the line passes through many points. But we only need 2 points in order to find the equation of the line. It can be any of the points as long as it is on the line.

So in our case let us use the points (-1, 0) and (0, -1) as our reference points.

STEP 2. Find the Slope "m".

The slope can be found using the formula;

`m=(y_2-y_1)/(x_2-x_1)`

where (x₁, y₁) and (x₂, y₂) are our reference ppoints (-1, 0) and (0, -1). Therefore our slope is:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=\frac{-1-0_{}}{0-(-1)_{}} \\ m=(-1)/(1) \\ m=-1 \end{gathered}`

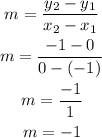
Therefore our slope is -1.

STEP 3. Use the Slope-Intercept Form to find the equation.

The Slope-Intercept Form is given by the formula:

`y=mx+b`

where x and y are any points in the line, m is the slope, and b is a constant.

Since we already have m which is -1, and we can find any points in the line as x and y we can now find the constant b.

Now using the point (-1, 0) as our reference point our equation now becomes:

`\begin{gathered} y=mx+b \\ 0=(-1)(-1)+b \\ 0=1+b \\ b=-1 \end{gathered}`

Therefore our b is -1.

Since we already have the constant b and our slope m. The equation of our line can now be represented by:

`\begin{gathered} y=mx+b \\ y=-1(x)-1 \\ y=-x-1 \end{gathered}`

Therefore the equation of our lines is:

`y=-x-1`