Question

Which of the following statements says that a number is between -3 and 3?

A. |x| < 3
B. |x| > 3

Answer 1

B! because X can represent any number, and your number(unknown) will be shown as X and for it to be in between both -3 and 3 it has to be less than (shown as >) 3 or greater than (shown as <) -3.

Answer 2

A. |x| < 3

Explanation:

The absolute value of a number is the value that a number has beyond its sign. This means that the absolute value is the numerical magnitude of the number regardless of whether its sign is positive or negative. Formally, the absolute value of any real number x, is defined by:

`|x|=\left \{ {{x,\hspace{3}if\hspace{3}x\geq0} \atop {-x,\hspace{3}if\hspace{3}x<0}} \right.`

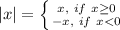
In this sense, to satisfy the inequality
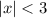`|x|<3`, the domain of x must be:

`-3<x<3\\\\or\\\\(-3,3)`

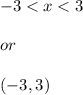
Because for
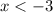`x<-3` or
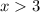`x>3` the inequality is absurd. For example if x=-4

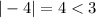`|-4|=4<3` which is not true.

and for x=4

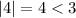`|4|=4<3` which is not true.

On the other hand to satisfy the inequality
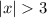`|x|>3`, the domain of x must be:

`-3>x>3\\\\or\\\\(-\infty,-3)\cup(3,\infty)`

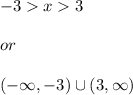
Because for
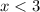`x<3` the inequality is absurd. For example if
`x=2`

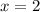
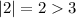`|2|=2>3` which is not true.

and for x=-1

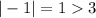`|-1|=1>3` which is not true.

Therefore the correct statement is:

A. |x| < 3