Hello
To solve this question, we have to write out equations.
Let x represent youth and y represent adults
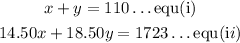
From equation (i), let's make x the subject of formula
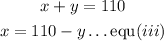
put equation (iii) into equation (ii)

now we havethe value of y, let's input this in equation (i) to solve for x
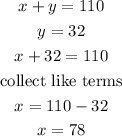
From the calculations above, the tickets sold for youth is 78 and adult is 32