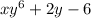Question

Find the quotient of the quantity negative 6 times x to the 2nd power times y to the 8th power plus 12 times x times y to the 3rd power minus 36 times x times y to the 2nd power all over 6 times x times y to the 2nd power.

Answer 1

The quotient is:

`xy^6+2y-6`

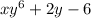
Explanation:

We are asked to find the quotient of the mathematical expression which is given in terms of variable x and y is represented as:

`=(6x^2y^8+12xy^3-36xy^2)/(6xy^2)`

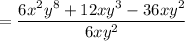
Here the numerator is:

`6x^2y^8+12xy^3-36xy^2`

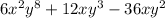
and the denominator is:

`6xy^2`

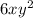
We can also represent our numerator term by the method of factoring it as:

`6x^2y^8+12xy^3-36xy^2=6xy^2(xy^6+2y-6)`

Hence, our expression gets converted by replacing the numerator term to:

`(6x^2y^8+12xy^3-36xy^2)/(6xy^2)=(6xy^2(xy^6+2y-6))/(6xy^2)\\\\(6x^2y^8+12xy^3-36xy^2)/(6xy^2)=xy^6+2y-6`

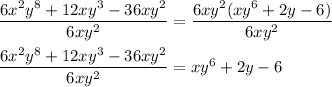
Hence, the quotient is:

`xy^6+2y-6`

Answer 2

[ - 6 * x^2 * y^8 + 12* x * y^3 - 36 * x * y^2 ] / [6*x*y^2] =

[-6x^2 y^8 ] / [6xy^2] + [12x y^3] / [6xy^2] - [36xy^2] / [6xy^2] =

- xy^6 + 2y - 6

Answer: - xy^6 + 2y - 6