Question

Assume that a simple random sample has been selected from a normally distributed population. State the hypotheses, find the test statistic, critical value(s) , P-value , and state the final conclusion.Test the claim that for the population of female college students, the mean weight is given by μ = 132 lb. Sample data are summarized as n = 20, overbar(x) = 137 lb, and s = 14.2 lb. Use a significance level of α = 0.1.

Answer 1

Hypotheses:

- The population mean is 132. In order to test the claim that the mean is 132, we should check for if the mean is not 132.

- Thus, the Hypotheses are:

`\begin{gathered} H_0:\mu=132 \\ H_1:\mu\\e132 \end{gathered}`

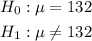
Test statistic:

- The test statistic has to be a t-statistic because the sample size (n) is less than 30.

- The formula for finding the t-statistic is:

`\begin{gathered} t=\frac{\bar{X}-\mu}{(s)/(√(n))} \\ \\ where, \\ \bar{X}=\text{ Sample mean} \\ \mu=\text{ Population mean} \\ s=\text{ Standard deviation} \\ n=\text{ Sample size} \end{gathered}`

- Applying the formula, we have:

`\begin{gathered} t=(137-132)/((14.2)/(√(20))) \\ \\ t=(5)/(3.1752) \\ \\ t\approx1.5747 \end{gathered}`

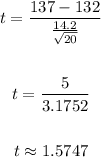
Critical value:

- The critical value t-critical, is gotten by reading off the t-distribution table.

- For this, we need the degrees of freedom (df) which is gotten by the formula:

`\begin{gathered} df=n-1 \\ df=20-1=19 \end{gathered}`

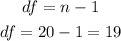
- And then we also use the significance level of 0.1 and the fact that it is a two-tailed test to trace out the t-critical. (Note: significance level of 0.1 implies 10% significance level)

- This is done below:

- The critical value is 1.729

P-value:

- To find the p-value, we simply check the table for where the t-statistic falls.

- The t-statistic given is 1.5747. We simply check which values this falls between in the t-distribution table. It falls between 1.328 and 1.729. We can simply choose a value between 0.1 and 0.05 and multiply the result by 2 since it is a two-tailed test.

- However, we can also use a t-distribution calculator, we have:

- Thus, the p-value is 0.13183

Final Conclusion:

- The p-value is 0.13183, and comparing this to the significance level of 0.1, we can see that 0.13183 is outside the rejection region.

- Thus, the result is not significant and we fail to reject the null hypothesis