Question

I sent pic for help. This question has 6 parts.

Answer 1

• (a)42%

,

• B. You have lost $16.

,

• (b) A. The change is consistent with the law of large numbers because as the number of trials increases, the proportion should grow closer to 50%.

,

• A. You have lost $36.

,

• (c)You would need to toss 68 heads. This is unlikely as it is far from the expected number of heads.

Explanation:

In the first 100 tosses, the number of outcomes are:

• Heads: 42

,

• Tails: 58

Part A

(a)The percentage of times heads have come up in the first 100 tosses is:

`42\%`

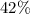
(b)You win $1 if a head appears and loses $1 if a tail appears.

`42(1)-58(1)=-\$16`

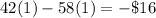
At this point: B)You have lost $16.

Part B

(c)By the law of large numbers, as the number of trials is increased, the result gets closer to the expected value.

Therefore, the change is consistent with the law of large numbers because as the number of trials increases, the proportion should grow closer to 50%.

Option A is correct.

(d)

There are a total of 300 tosses.

Head comes up 44% of the time.

`\begin{gathered} Head(Gain):300*(44)/(100)=132 \\ Tails(Loss):300*(56)/(100)=168 \\ Net\text{ Loss=132-168=\$36} \end{gathered}`

A. You have lost $36.

Part C

So far, out of 300 tosses, there are 132 Heads.

In order to break even after 400 tosses, the number of heads must be equal to the number of tails.

Therefore:

`200-132=68`

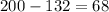
Therefore, you would need to toss 68 heads. This is unlikely as it is far from the expected number of heads.

Option B is correct.