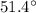Question

What is the measure of an exterior angle of a regular 7-sided polygon?

Enter your answer as a decimal in the box.

Round to the nearest tenth of a degree.

Answer 1

Answer:
`51.4^(\circ)`

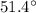
Explanation:

We know that the sum of all the exterior angles of a regular polygon with n sides is
`360^(\circ)`.

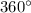The measure of an exterior angle of a regular n-sided polygon is given by :-

`(360^(\circ))/(n)`

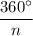
Now, the measure of an exterior angle of a regular 7-sided polygon is given by :-

`(360^(\circ))/(7)=51.4285714286^(\circ)\approx51.4^(\circ)`

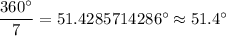
Hence, the measure of an exterior angle of a regular 7-sided polygon =
`51.4^(\circ)`

Answer 2

The sum of internal angles in an n-sided polygon is 180(n-2).

In a regular 7-sided polygon, the sum of the internal angles is
180*(7 - 2) = 900°
Each internal angle is 900/7 = 128.57°.

Because the sum of angles on one side of a straight line is 180°. therefore
each exterior angle is 180 - 128.57 = 51.43°

Answer: 51.4° (nearest tenth)