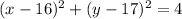The equation of a circle with center (h,k) and radius r is:
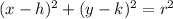
Since the center is (16,17), then h=16 and k=17. The radius is the distance from the circle to any of the points on the circumference. Find the distance between (16,17) and (14,17). Since that is the distance between the center and a point on the circumference, then, the result will tell us the radius.
Use the formula to find the distance between two points:
![\begin{gathered} d=\sqrt[]{(16-14)^2+(17-17)^2} \\ =\sqrt[]{2^2+0^2} \\ =\sqrt[]{2^2} \\ =2 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/rlq8p7mdr2h9iuq40b0m.png)
Then, r=2. Substitute the values of h, k, and r into the equation of a circle:
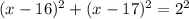
This can also be written as: