Question

Find the composition of transformationsthat map APQR to AP'Q'R'.RДΓΡ. ΤΟ.Reflect over [ ? ) andthen translateunit(s)to the [].P'QR'X-axisy-axis

Answer 1

Reflect over the x axis, then translate 2 units to the left

Step-by-step explanation:

To determine the transformationthat occured fromPQR to P'Q'R', we will use the coordinates of each letter and compare

P = (1, 1), Q = (2, 1) and R = (2, 3)

P' = (-1, -1), Q' = (0, -1) and R' = (0, -3)

We can see the y axis of P, Q, and R were negated to obtain the y axis of P', Q' and R.

`\begin{gathered} (x,\text{ y) }\rightarrow\text{ (x, -y)} \\ \text{This is a reflection over the x ax is} \end{gathered}`

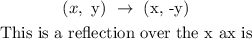
The translation that occurred on the x coordinates:

`\begin{gathered} \text{After the reflection on PQR, we have: (1, -1), (2, -1) and (2, -3)} \\ \text{The translation on the x coordinate:} \\ (1,\text{ -1): (1 - 2, 1) = (-1, -1)} \\ P^(\prime)\text{ = (-1, -1)} \\ (2,\text{ -1): (2 - 2, -1) = (0, -1)} \\ Q^(\prime)\text{ = (0, -1)} \\ (2,\text{ -3): (2-2, -3) = (0, -3)} \\ R^(\prime)\text{ = (0, -3)} \end{gathered}`

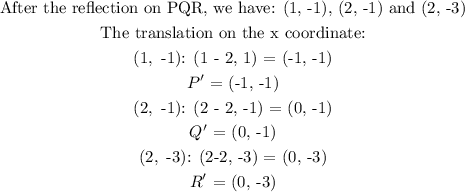
From the above, 2 units was subtracted from the x coordinate of PQR to obtain the x coordinate of P'Q'R'.

Subtraction indicate movement is to the left

After the reflection over the x axis, there is a translation of 2 units to the left