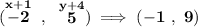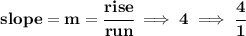
so the rise is 4 units and the run is 1 unit, ok.
now, from point -2, 5, if we move 4/1, that is, "1 unit over the x-axis, and 4 units over the y-axis", we'll find another point, now, a fraction can be positive so long both top and bottom are the same sign, so -4/-1 is the same as 4/1 and therefore, if we move +4 and +1 over the axes we get a point, or if we move -4 and -1 we also get another point, and any other subsequent points from there on.
so, hmm let's check