Question

Divide and write the result in standard form: 3-i/1+5i

A. 1/13 +8/13i
B. -1/13+8/13i
C. 1/13-8/13i
D. -1/13-8/13i

Answer 1

We are asked to write the following fraction of complex numbers in standard form:
`\displaystyle{ (3-i)/(1+5i)`.


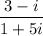
Whenever we are dividing by a complex number by another complex number a+bi, to write the result in standard form, we multiply the expressions in the numerator and denominator by the conjugate of a+bi, that is a-bi:



`\displaystyle{ (3-i)/(1+5i)= ((3-i)(1-5i))/((1+5i)(1-5i))`

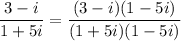
in the numerator we distribute (3-i) to 1 and -5i, in the denominator we use the difference of squares formula
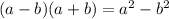
`(a-b)(a+b)=a^2-b^2`, and
`i^2=-1`:


`\displaystyle{ ((3-i)(1-5i))/((1+5i)(1-5i))= ((3-i)\cdot1+(3-i)\cdot(-5i))/(1^2-(5i)^2)= (3-i-15i-5)/(1-25i^2)`


`\displaystyle{= (-2-16i)/(1+25)= (-2-16i)/(26)=-1/13-(8/13)i`

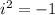
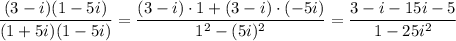
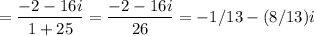
Answer: D